728x90
📌문제 출처
백준 단계별 문제풀이 - 동적 계획법 2단계
https://www.acmicpc.net/problem/11049
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
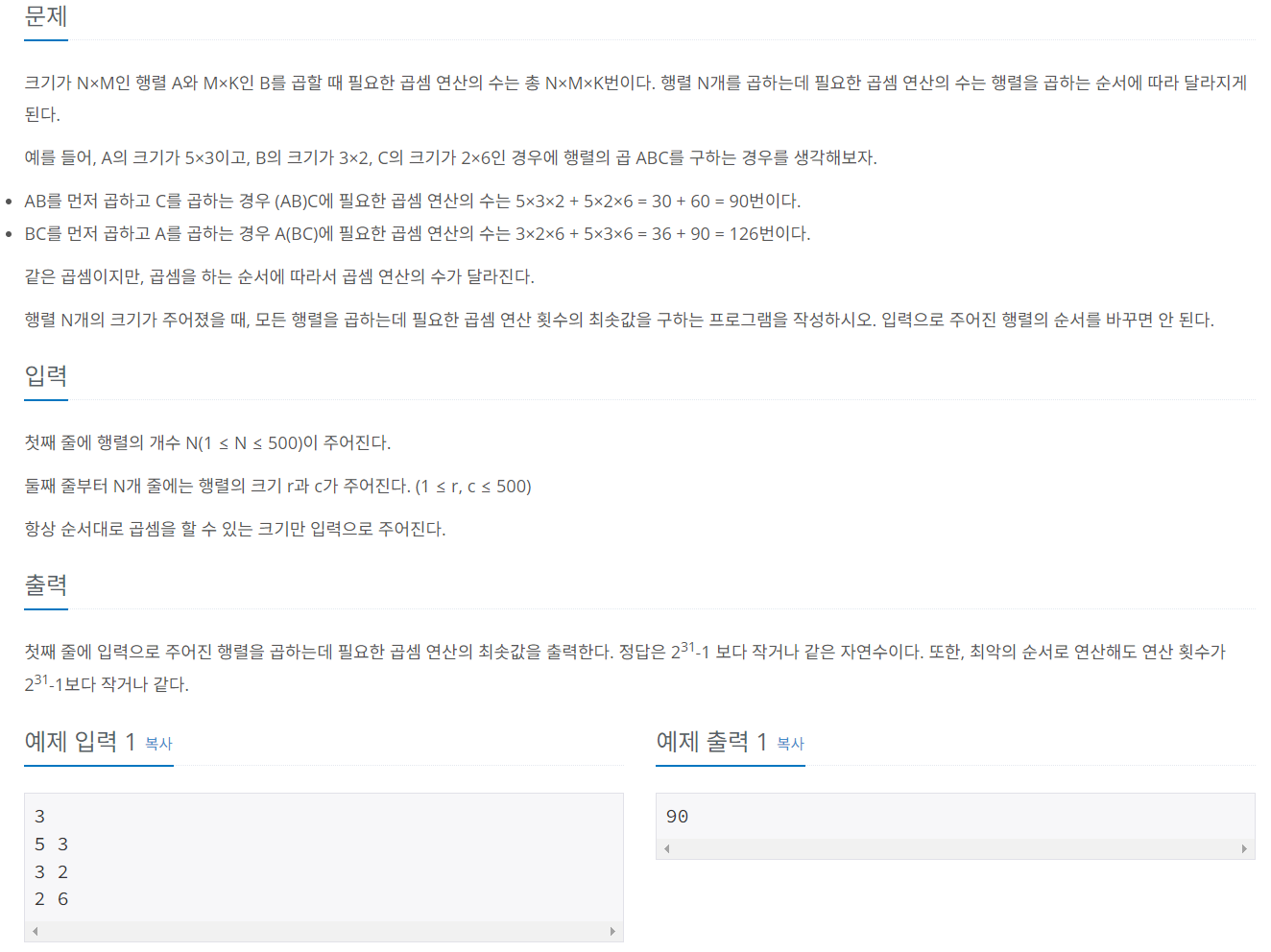
❓ 문제
❗ 풀이
- 동적계획법 2단계 11066 파일합치기와 유사한 풀이 활용
https://nembizzang.tistory.com/135
📗 풀이 코드
import sys
input = sys.stdin.readline
n = int(input())
nums = [list(map(int,input().split())) for _ in range(n)]
dp = [[0]*(n+1) for _ in range(n+1)]
for i in range(1,n): # 간격
for j in range(1,n-i+1): # 시작점
s,e = j,j+i
tmp = nums[s-1][0]*nums[e-1][1] # 반복되는 연산을 미리 처리
dp[s][e] = min([dp[s][k] + dp[k+1][e] + tmp*nums[k-1][1] for k in range(s,e)])
print(dp[1][n])📗 코드 해설
- 연속적으로 두개씩 합쳐야하므로 이 문제는 전체 행렬 중에서 어떤 행렬을 먼저 곱할지 부분을 나누는 문제이다.
- 2개부터 시작해서 1개씩 추가로 합쳐가며 가능한 경우의 최소값을 추가해나가기에 전체를 부분의 문제로 나누어서 푸는 동적계획법이 될 수 있다.
- 1,2,3 인덱스의 행렬이 있다고 할때 (1,2)를 먼저 합치고 3을 합치는 경우와 (2,3)을 먼저 합치고 1을 합치는 경우가 있다. 이때 각각의 경우를 연산하고 최종값의 최소값을 구한다. 이를 이어서 네개의 경우일 때 (1개, 3개), (2개,2개)로 나누는 경우로 확장해서 생각을 해보자.
- 다음과 같이 예제에서 하나의 행렬을 추가한 케이스를 생각해보자
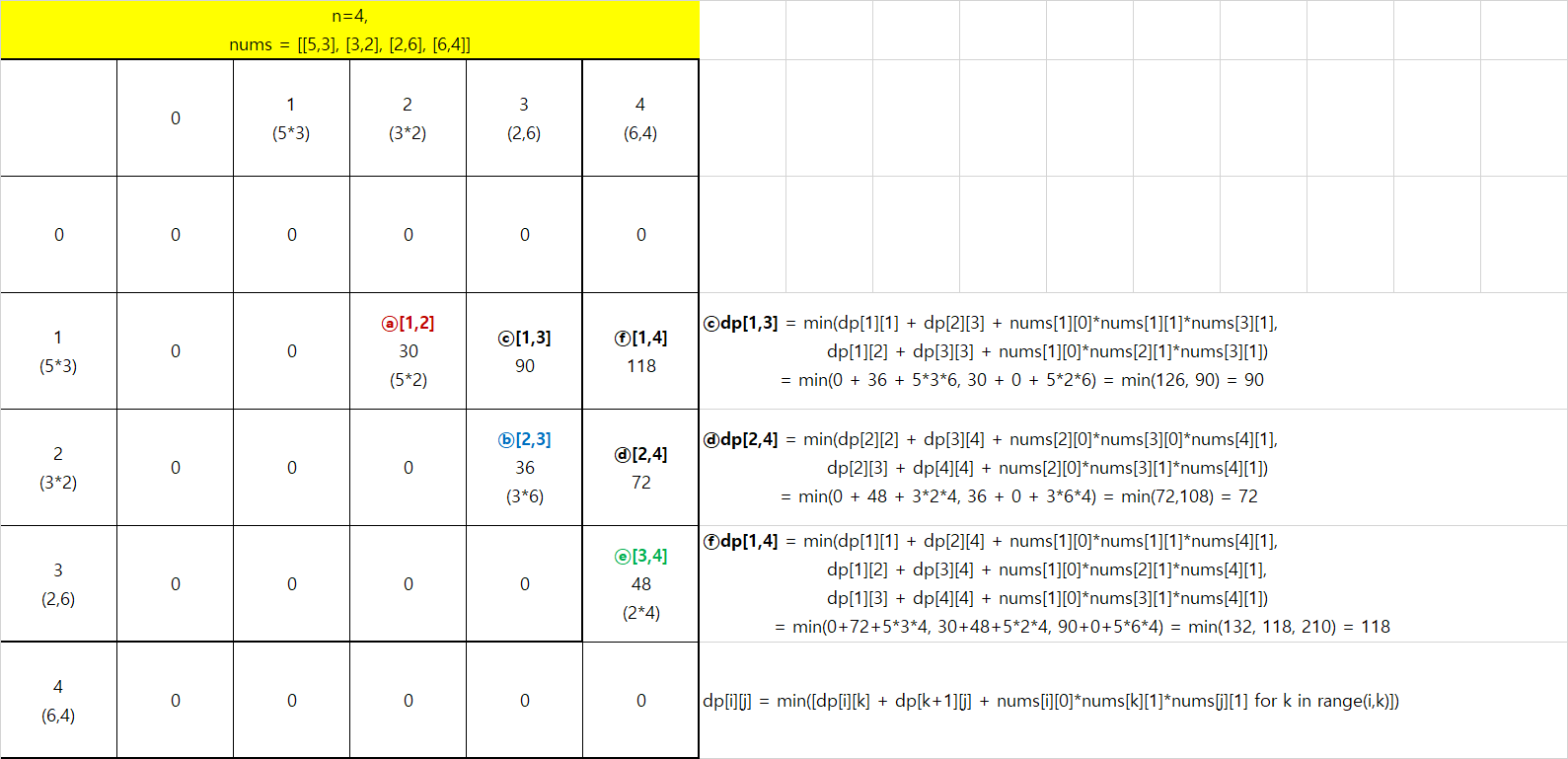
- dp[1][3], 즉 첫번째부터 세번째 행렬을 합치는 경우는 1,(2~3) / (1,2),3 로 두가지 경우가 있다.
합치는 경우가 아닌 1과 3을 그냥 불러오는 경우에는 연산이 없으므로 dp[1][1][ = dp[3][3] = 0 이다.
이 때 최소값을 구할 때에는 행렬 연산의 개수를 구해줘야하므로 첫번째 행렬의 행과 열의 곱에 두번째 행렬의 열을 곱한 값을 더해주어야한다.(첫번째 행렬의 열 = 두번째 행렬의 행이기에 첫번째 행렬의 열로 통일) - 이를 dp[1][4], 즉 첫번째부터 네번째 행렬을 모두 합치는 경우로 생각해보자
경우는(1~3),4 / (1~2),(3~4) / 1,(2~4)로 나눌 수 있고 이는 앞서 구한 1~2, 3~4, 1~3, 2~4를 사용하여 연산 가능하다. - 최종적인 점화식은 다음과 같다.
dp[i][j] = min([dp[i][k] + dp[k+1][j] + nums[i][0]*nums[k][1]*nums[j][1] for k in range(i,j)])- 이를 코드로 적용할 때 nums[i][0]*nums[j][1]은 해당 리스트에서 고정값이므로 연산속도를 줄여주기 위하여 미리 구해놓는다.
- dp를 생성하는 반복문은 다음과 같은 순서로 행과 열을 확인한다.
n=4일때, dp 순환
1) i=1 : j는 1~3까지 / j=1 : dp[1][2] / j=2 : dp[2][3] / j=3 : dp[3][4]
2) i=2 : j는 1~2까지 / j=1 : dp[1][3] / j=2 : dp[2][4]
3) i=3 : j는 1~1까지 / j=1 : dp[1][4]
'파이썬 문제풀이' 카테고리의 다른 글
| [백준 파이썬] 7576 토마토 (1) | 2023.09.06 |
|---|---|
| [백준 파이썬] 2629 양팔저울 (0) | 2023.09.06 |
| [백준 파이썬] 1074 Z (0) | 2023.09.01 |
| [백준 파이썬] 2475 검증수 (0) | 2023.08.31 |
| [백준 파이썬] 1003 피보나치 함수 (0) | 2023.08.31 |