728x90
📌문제 출처
솔브닷 클래스 4
https://www.acmicpc.net/problem/1167
1167번: 트리의 지름
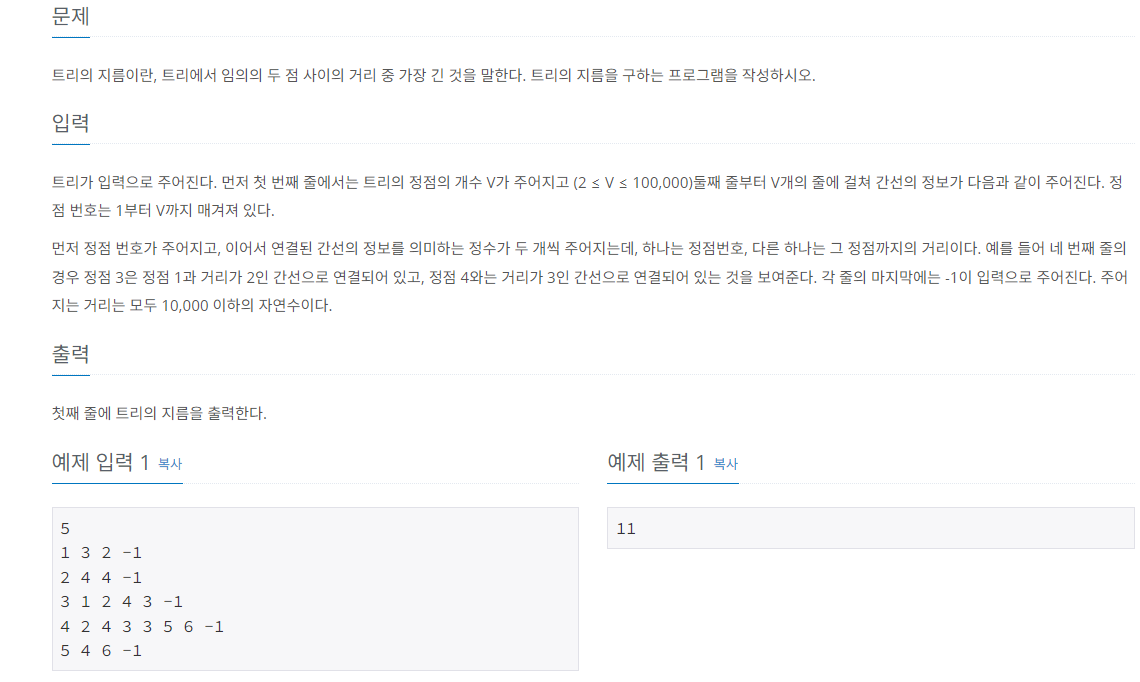
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
❓ 문제
📗 풀이 코드
'''
트리 구조에서 임의의 한 노드로부터 가장 멀리 떨어진 노드는 반드시 트리의 지름 중 한 노드이다.
따라서 임의의 한 노드부터 가장 멀리 떨어진 노드를 구하고 그 노드로부터 가장 멀리 떨어진 노드까지의 거리를 구하자.
1) bfs 함수 생성
node로부터 가장 멀리 떨어진 노드를 반환하는 함수
def bfs(node,flag=False): node:방문노드, cur_dist:현재이동거리, True면 멀리 떨어진 거리 반환
visited = defaultdict(int) : 방문 확인
end_node = dist = 0 : 가장 멀리떨어진 노드와 거리 초기화
queue = deque([[node,0]])
while queue:
cur_node,cur_dist = queue.popleft()
if 문 : dist < cur_dist라면 end_node, dist 초기화
visited[cur_node] = 1 방문 확인
for 문 : tree[cur_node]에서 new_node, new_dist 하나씩 반복
if new_node가 최초방문이라면
queue.append([new_node,cur_dist+new_dist])
if 문 : flag가 true면
return dist
return end_node
2) 입력값 받기, 변수 선언
v = 노드 개수
tree = {}} : v개 노드별 간선 정보를 [노드,거리] 형태로 담아두기
3) bfs 진행
return bfs(bfs(1),True) : 임의노드(1)로부터 가장 멀리 떨어진 노드로부터 가장 멀리 떨어진 노드까지의 거리
'''
from collections import defaultdict, deque
input = open(0).readline
# 1) bfs 함수 생성
def bfs(node,flag=False): # node:방문노드, cur_dist:현재이동거리, True면 멀리 떨어진 거리 반환
visited = defaultdict(int) # 방문 확인
end_node = dist = 0 # 가장 멀리떨어진 노드와 거리 초기화
queue = deque([[node,0]])
while queue:
cur_node,cur_dist = queue.popleft()
if dist < cur_dist :
end_node,dist = cur_node,cur_dist # end_node와 dist 초기화
visited[cur_node] = 1 # 방문 확인
for new_node, new_dist in tree[cur_node] : # new_node, new_dist 하나씩 반복
if not visited[new_node] :
queue.append([new_node,cur_dist+new_dist])
if flag :
return dist
return end_node
# 2) 입력값 받기, 변수 선언
def solution():
global tree
v = int(input()) # 노드 개수
tree = {} # v개 노드별 간선 정보를 [노드,거리] 형태로 담아두기
for _ in range(v):
node,*lines,_ = list(map(int,input().split()))
tree[node] = [lines[2*i:2*i+2] for i in range(len(lines)//2)] # lines의 길이는 이어진 노드 개수의 두배
# 3) bfs 진행
return bfs(bfs(1),True) # 임의노드(1)로부터 가장 멀리 떨어진 노드로부터 가장 멀리 떨어진 노드까지의 거리
if __name__ == '__main__':
print(solution())'파이썬 문제풀이' 카테고리의 다른 글
| [백준 파이썬] 12852 1로 만들기 2 (1) | 2023.11.29 |
|---|---|
| [백준 파이썬] 1238 파티 (0) | 2023.11.24 |
| [백준 파이썬] 1043 거짓말 (1) | 2023.11.20 |
| [백준 파이썬] 1450 냅색문제 (1) | 2023.10.26 |
| [백준 파이썬] 1806 부분합 (0) | 2023.10.25 |