728x90
📌문제 출처
백준 단계별 문제풀이 - 분할정복
https://www.acmicpc.net/problem/1629
1629번: 곱셈
첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.
www.acmicpc.net
❓ 문제
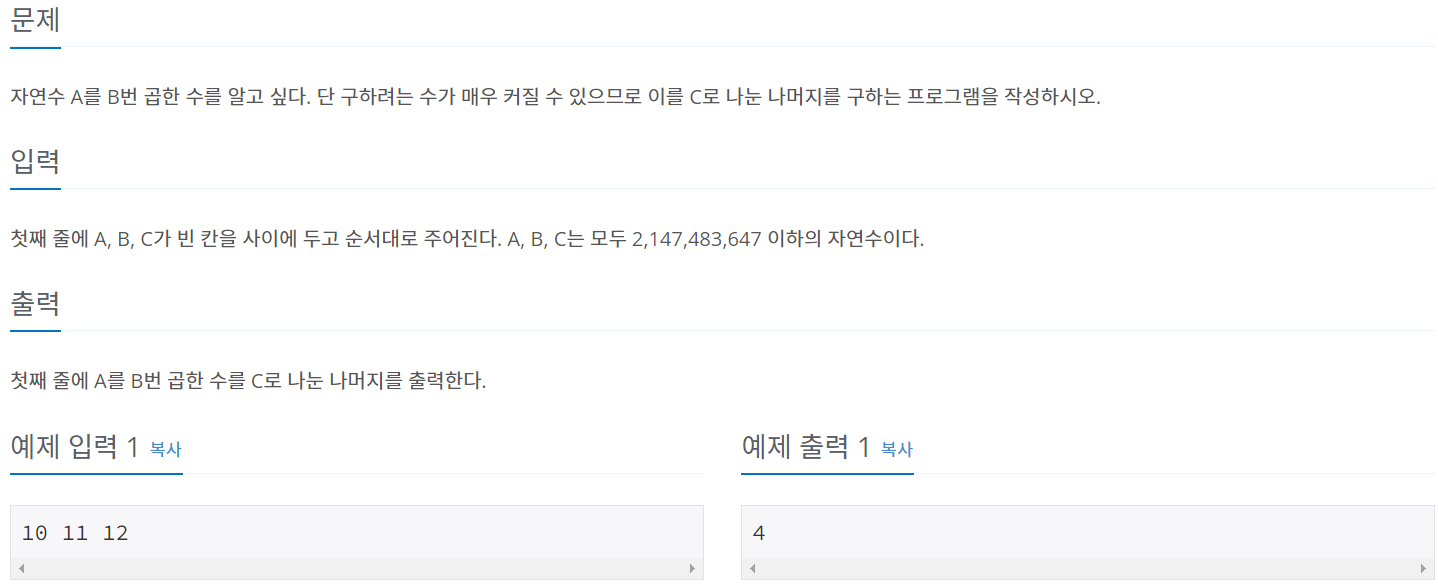
❗ 풀이
- (a**n)%c == (((a**(n-1))%c)*a)%c라는 성질 이용
📗 풀이 코드
import sys
input = sys.stdin.readline
a,b,c = map(int,input().split())
rests = [] # a**i의 나머지 집합
i = 1
rests.append(a%c)
# rests에는 a**1의 나머지, a**2의 나머지, a**4의 나머지, a**8의 나머지...가 들어간다.
while i <= b:
rests.append((rests[-1]**2)%c)
i *= 2
ans = 1
for rest,i in zip(rests,bin(b)[2:][::-1]): # b의 2진법을 뒤집었다.
if int(i):
ans = (ans*(rest*int(i))%c)%c
print(ans)📗 코드 해설
- 연산 횟수를 줄이기 위해 a를 2의 거듭제곱만큼 곱한 수의 나머지를 저장해둔다.
- ((a**n%c)**2)%c = ((a**(n**2)%c)를 이용하여 rests에 나머지를 저장
- b를 2진법으로 나타내면 위에서 만든 rests들의 나머지 중 어떤 것들이 곱해져야 b번 곱한 효과가 나는지 확인가능
- b를 2진법으로 변경 후 작은 수부터 시작하여 a를 1번, 2번,4번,... 곱해서 총 b번 곱해질 때까지의 나머지를 구한다.
- pow(a,b,c)를 사용하면 a**b%c를 빠르게 구할 수 있다.
'파이썬 문제풀이' 카테고리의 다른 글
| [백준 파이썬] 10830 행렬 제곱 (0) | 2023.08.10 |
|---|---|
| [백준 파이썬] 2740 행렬 곱셈 (0) | 2023.08.07 |
| [백준 파이썬] 1992 쿼드트리 (0) | 2023.08.05 |
| [백준 파이썬] 2630 색종이 만들기 (0) | 2023.08.03 |
| [백준 파이썬] 13305 주유소 (0) | 2023.08.03 |