728x90
📌문제 출처
백준 단계별 문제풀이 : 동적 계획법과 최단거리 역추적
https://www.acmicpc.net/problem/14002
14002번: 가장 긴 증가하는 부분 수열 4
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
❓ 문제
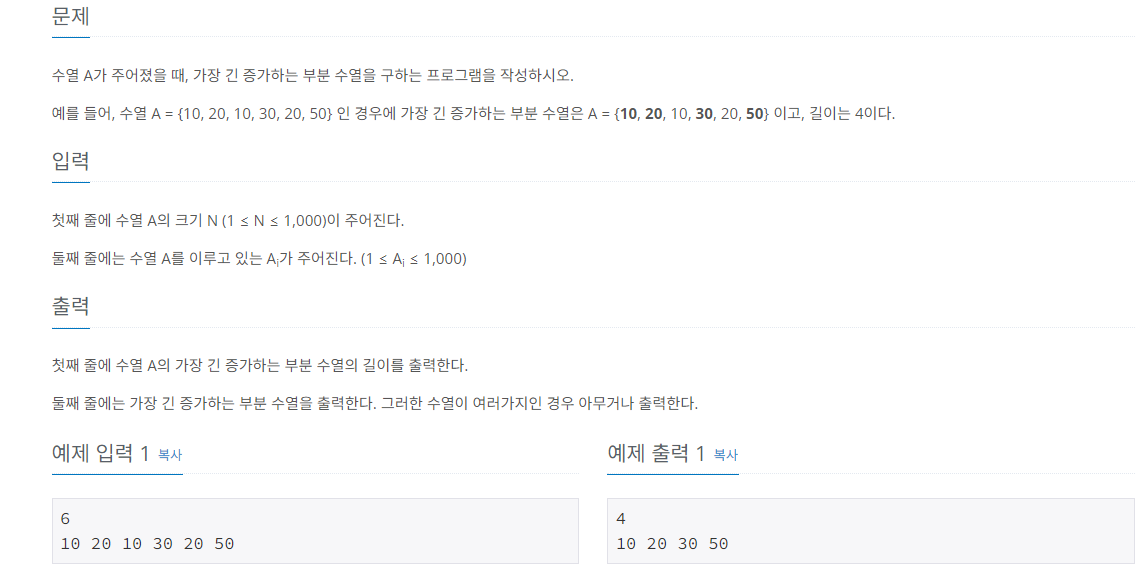
📗 풀이 코드
'''
dp = 해당 인덱스의 수가 마지막일때 가장 긴 증가하는 부분 수열의 길이, 최초는 1
수열의 수를 하나씩 뽑아서 그 수의 바로 직전까지 이중 for문을 반복하여 dp를 완성한다.
1) 변수 선언
n = 수열 A의 크기
nums = 수열 A list
max_idx, max_num = 최대 부분 증가 수열 끝 인덱스, 최대 부분 증가 수열의 길이, 최초 0,1
2) dp 채우기
for i in range(n) : i는 수열 A의 인덱스
for j in range(i-1) : i를 기준으로 직전 인덱스까지 확인
if nums[j] < nums[i] and dp[i] < dp[j]+1 : 기준 수가 이번 수보다 크고
j까지 확인한 부분 증가 수열의 길이를 1 늘리는게 지금까지 최대라면
dp[i] = dp[j]+1 j까지 확인한 부분 증가 수열의 길이를 1 늘리기 or 지금 dp 그대로
if max_num < dp[i] : 최대 길이가 갱신되었다면
max_num = dp[i]
max_idx = i
print(max_num)
3) 최대 부분 증가 수열 찾기
new_nums = 최대 부분 증가 수열 list, 최초값은 nums[max_idx]
for i in range(max_idx-1,-1,-1) : 마지막 인덱스부터 거꾸로 확인하며
dp[i]가 max_num보다 1이 작다면(부분 수열의 길이가 1 작다면)
new_nums.append(new_nums[ㅑ]) 갱신된 최대 인덱스의 새로운 수 추가
max_num -= 1 최대 길이 초기화
4) 정답 출력
print(reverse(new_nums))
return
'''
input = open(0).readline
def solution():
# 1) 변수 선언
n = int(input())
nums = list(map(int,input().split()))
max_idx,max_num = 0,1 # 최대 부분 증가 수열 끝 인덱스, 최대 부분 증가 수열의 길이, 최초 0,1
dp = [1]*n
# 2) dp 채우기
for i in range(1,n) : # i는 수열 A의 인덱스
for j in range(i) : # i를 기준으로 직전 인덱스까지 확인
# 기준 수가 이번 수보다 크고 j까지 확인한 부분 증가 수열의 길이에서 1 늘리는게 지금까지 최대라면
if nums[j] < nums[i] and dp[i] < dp[j]+1 :
dp[i] = dp[j]+1 # j까지 확인한 부분 증가 수열의 길이를 1 늘리기
if max_num < dp[i] : # 수열 최대 길이가 갱신되었다면 최대 길이, 최대 인덱스 갱신
max_num = dp[i]
max_idx = i
print(max_num)
# 3) 최대 부분 증가 수열 찾기
new_nums = [nums[max_idx]] # 최대 부분 증가 수열 list, 최초값은 nums[max_idx]
for i in range(max_idx-1,-1,-1) : # 마지막 인덱스부터 거꾸로 확인하며
if dp[i] == max_num-1 : # 최대 부분 증가 수열의 다음 수를 찾았다면
new_nums.append(nums[i]) # 갱신된 최대 인덱스의 새로운 수 추가
max_num -= 1
# 4) 정답 출력
print(*new_nums[-1::-1])
if __name__ == '__main__':
solution()'파이썬 문제풀이' 카테고리의 다른 글
| [백준 파이썬] 1967 트리의 지름 (1) | 2023.12.01 |
|---|---|
| [백준 파이썬] 11725 트리의 부모찾기 (1) | 2023.11.29 |
| [백준 파이썬] 12852 1로 만들기 2 (1) | 2023.11.29 |
| [백준 파이썬] 1238 파티 (0) | 2023.11.24 |
| [백준 파이썬] 1167 트리의 지름 (1) | 2023.11.24 |