728x90
📌문제 출처
백준 단계별 문제풀이 : 기하2
https://www.acmicpc.net/problem/1069
1069번: 집으로
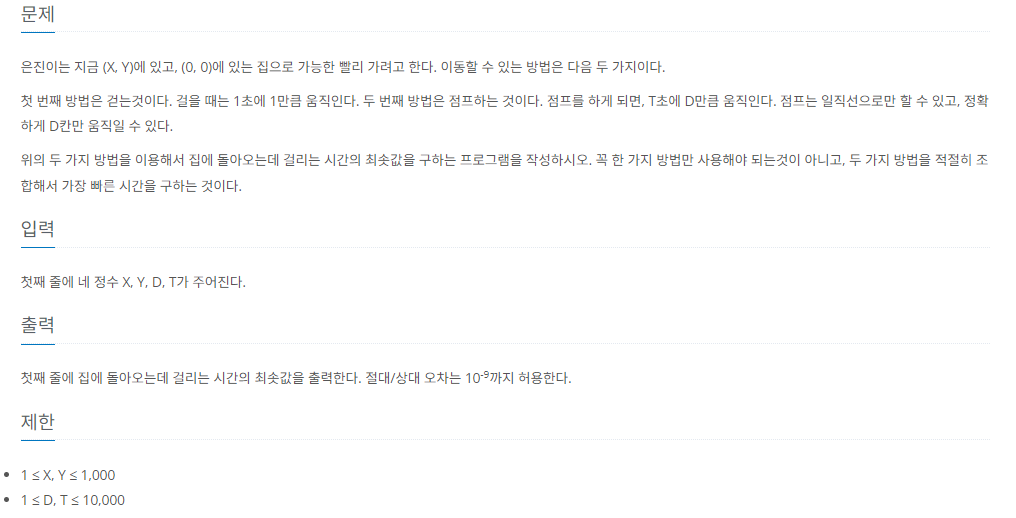
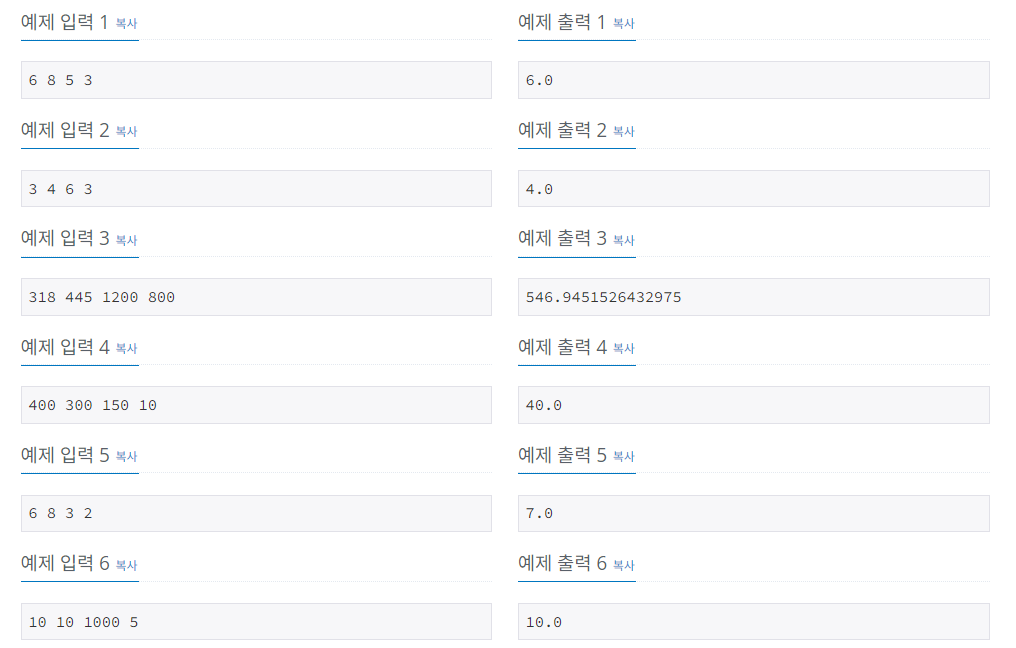
은진이는 지금 (X, Y)에 있고, (0, 0)에 있는 집으로 가능한 빨리 가려고 한다. 이동할 수 있는 방법은 다음 두 가지이다. 첫 번째 방법은 걷는것이다. 걸을 때는 1초에 1만큼 움직인다. 두 번째 방법
www.acmicpc.net
❓ 문제
📗 풀이 코드
'''
1) 걷기만 하는 것이 빠른 경우(자명한 경우)
- 직선 거리(= 걷기만 해서 도착하는 시간) <= T 인 경우
- T>=D인 경우(걸음 자체가 점프보다 빠름)
최소 도달 시간 = 직선 거리
2) 점프만 하는 것이 빠른 경우(자명한 경우)
- 직선 거리가 D의 정수 배인 경우
최소 도달 시간 = ((직선 거리)//D)*t
3) 걷기와 점프를 합치거나, 조건 비교 해야하는 경우(아래 세 값 중 최소값 사용)
a. 직선 경로(점프 + 걷기)
1) 점프로 일직선 상에서 최대한 진행 후 남은 거리 걸어서 가기
j(점프 횟수) = (직선 거리//D), w(걷는 횟수) = (직선 거리)-j*D, 최소 도달 시간 = j*T + w
2) 위 경우에서 점프를 한 번 더 하고 넘치는 거리 걸어서 돌아오기
j = (직선거리//D)+1, w = j*D - (직선 거리), 최소 도달 시간 = j*T + w
b. 직선 + 우회 경로(점프만)
1) 점프로 최대한 진행 후 점프 두번으로 이등변 삼각형 형태로 우회하기
j = (직선 거리//D)+1, 최소 도달 시간 = j*T
2) b1과 같은 상황이나 직선 거리 < d 인 경우 => 시작부터 이등변 삼각형을 만들어야 한다.
j = 2, 최소 도달 시간 = 2*T
'''
input = open(0).readline
def solution():
x,y,d,t = map(int,input().split())
dist = round((x**2+y**2)**0.5,10) # 직선거리
if dist <= t or t>=d : # 걷기만 하는 것이 빠른 경우
return dist
if not dist%d : # 점프만 하는 것이 빠른 경우
return (dist//d)*t
# a1 경우
j1 = dist//d
w1 = dist-j1*d
# a2 경우
j2 = dist//d + 1
w2 = j2*d-dist
# a3 경우
j3 = dist//d + 1 if dist > d else 2
return min(j1*t + w1, j2*t + w2, j3*t)
if __name__ == '__main__':
print(solution())
✍ 추가 설명
자명한 두가지 경우를 제외한 비교 조건을 따져야하는 경우는 다음과 같다.


'파이썬 문제풀이' 카테고리의 다른 글
| [백준 파이썬] 1311 할 일 정하기 1 (1) | 2024.01.11 |
|---|---|
| [백준 파이썬] 11723 집합 (1) | 2024.01.10 |
| [백준 파이썬] 7869 두 원 (1) | 2024.01.09 |
| [백준 파이썬] 17387 선분 교차 2 (1) | 2024.01.09 |
| [백준 파이썬] 17386 선분 교차 1 (0) | 2024.01.09 |