728x90
📌문제 출처
백준 단계별 문제풀이 : 동적계획법 3
https://www.acmicpc.net/problem/1311
1311번: 할 일 정하기 1
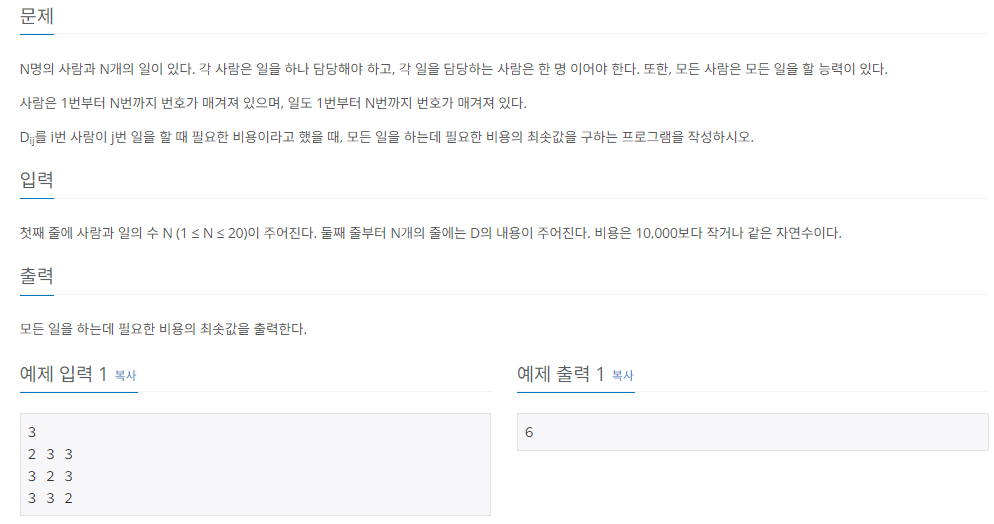
N명의 사람과 N개의 일이 있다. 각 사람은 일을 하나 담당해야 하고, 각 일을 담당하는 사람은 한 명 이어야 한다. 또한, 모든 사람은 모든 일을 할 능력이 있다. 사람은 1번부터 N번까지 번호가 매
www.acmicpc.net
❓ 문제
📗 풀이 코드
* pypy3로 제출 시 성공(python 3는 시간 초과)
'''
기본적으로 dfs+dp 문제이나, 방문확인을 하는 방법이 복잡하기에 비트마스크를 활용하는 방법이다.
dfs를 통해 일의 개수와 일하는 사람 수를 늘려가면서
해당 일까지 일을 참여한 사람이 모두 일할 수 있는 조합 중 최소값을 찾아서 dp에 저장해두자.
예를 들어 세번째 일까지 1,2,3 번 사람들이 모두 할 수 있는 조합은 123,132,213,231,312,321 6가지가 있다.
그리고 dp = 일의 개수*((2**n)-1)의 크기로 만들어준다.
이를 통해서 일을 참여한 사람들을 비트로 표현해주고 그것을 십진수로 변환 후 해당 인덱스의 dp에
앞서 찾은 조합 중 최소값을 저장해줄 것이다.
예를 들어 dp[3]의 경우 일이 세가지이기 때문에 최대 세 사람까지 일할 수 있다.
n=3인 경우에는 일하는 사람을 표시하는 경우는 111이고, 이 경우 중 조합을 따져 최소값을 dp에 넣어둔다.
즉 111->7이므로 dp[3][7] = 123,132,213,231,312,321 6가지 조합 중 최소값이 적용된다.
비트마스크를 사용하는 이유는 방문 확인을 획기적으로 빠르게 할 수 있기 때문이다.
list나 dict를 활용한 방문 확인의 경우 이런 복잡한 상황에서는 n!개수만큼 방문 확인을 해줘야하는데,
비트마스크를 활용하면 (2**n)-1의 정수 하나로 모든 경우를 표현할 수 있기 때문이다.
'''
input = open(0).readline
def solution():
n = int(input())
jobs = [list(map(int,input().split())) for _ in range(n)]
max_ = 10000*n+1 # 모두가 10000짜리 일을 했을 경우의 최대값+1
dp = [[max_]*((1<<n)-1) for _ in range(n)] # n개의 행마다 n개의 비트를 표현할 수 있게 만들어줌
def dfs(nth_jobs,visit): # n_jobs는 확인하는 일의 순서, visit은 방문확인용 비트
# 종료 조건 1
if visit == (1<<n)-1 : # 모두가 일을 참여하는 경우(방문확인이 11111111)까지 확인했을 시
return 0 # 더이상 할 수 있는 일이 없으므로 종료
# 종료 조건 2
if dp[nth_jobs][visit] != max_ : # 메모이제이션된 값이 있을 경우
return dp[nth_jobs][visit]
# dfs
for i in range(n): # 다음 일들을 순서를 하나씩 늘려가며 확인
bit = 1 << i # bit는 사람을 표현 => 첫 사람부터 끝 사람까지 일 했는지 방문확인
if visit&bit : # 이미 방문한 적이 있다면
continue # 다음 사람 방문 확인
# 방문한 적이 없다 => 해당 visit의 사람들이 일을 할 수 있다.
# nth_jobs일까지 visit 사람들이 일했을 때의 최소값 = min(지금 값, dfs를 통해 향후 진행되는 것들 중 최소값)
dp[nth_jobs][visit] = min(dp[nth_jobs][visit],dfs(nth_jobs+1,visit|bit)+jobs[nth_jobs][i])
return dp[nth_jobs][visit]
print(dfs(0,0)) # 모두가 빠짐없이 일을 했을 때의 최소값을 출력
if __name__ == '__main__':
solution()
✍ 추가 설명
예제 1번을 위의 코드로 작동 시 완성된 dp는 다음과 같다.
dfs를 끝까지 진행해서 마지막 행을 완성 후 해당 결과를 이전 단계 재귀함수에 반환해서 맨 위의 결과까지 올라온다.

'파이썬 문제풀이' 카테고리의 다른 글
| [백준 파이썬] 17404 RGB거리 2 (0) | 2024.01.12 |
|---|---|
| [백준 파이썬] 1149 RGB거리 1 (0) | 2024.01.12 |
| [백준 파이썬] 11723 집합 (1) | 2024.01.10 |
| [백준 파이썬] 1069 집으로 (0) | 2024.01.09 |
| [백준 파이썬] 7869 두 원 (1) | 2024.01.09 |